引言
铅冷快堆(LFR)是第四代核能国际论坛(GIF)确立的6种第四代反应堆之一[1]。螺旋盘管型直流蒸汽发生器结构紧凑,换热能力强,因此国际上一些铅冷快堆选择其作为主换热器[2-3]。流致振动现象广泛存在于蒸汽发生器中,从而导致微动磨损现象出现,严重时将导致蒸汽发生器传热管破裂事故,威胁反应堆安全[4]。国内外对蒸汽发生器传热管的流致振动问题越发关注,一些学者针对螺旋盘管管束开展流致振动实验与数值研究[5-6],研究发现增加上下游管束将增加振动频率,但是会导致振动响应相对减少。Jung等人[7-8]研究了曲率管面内与面外的振动特性,发现了面外方向上出现了倍频现象,同时不稳定区域的大小也会随流速的增大而增大。管内流动所产生的振动多为较高频率的微动,这类振动更易诱发微动磨损[9-10]。因此,很多学者针对螺旋盘管内流致振动开展了一系列研究。Tang等[11]建立了弯曲微管的振动理论模型,该模型同时考虑面内与面外的振动,并基于拉格朗日非线性轴向应变来获得管内流体流动所产生的静变形。
Ibrahim[12]认为管内流致振动的本质上是由于惯性力、弹性力以及离心力相互作用导致的。目前针对螺旋盘管内流致振动相关研究主要关注盘管的振动响应特征,而管内流体流动状态对振动响应间的内在联系尚未厘清,无法提出更具普适性的振动机制。因此亟需开展相关研究,探究管内流体流动状态对振动响应的影响机制。本研究基于激光多普勒测量技术,开展螺旋盘管内单相流致振动实验,获得振动响应实验数据,结合模态分析,探究沿面内及面外的振动响应特性,明晰了影响螺旋盘管振动响应的关键因素,揭示了管内流体对振动响应的影响机制。本实验可为螺旋盘管内流致振动研究提供参考,并可为后续管内两相流致振动研究提供支撑。
1、实验方法
1.1实验回路
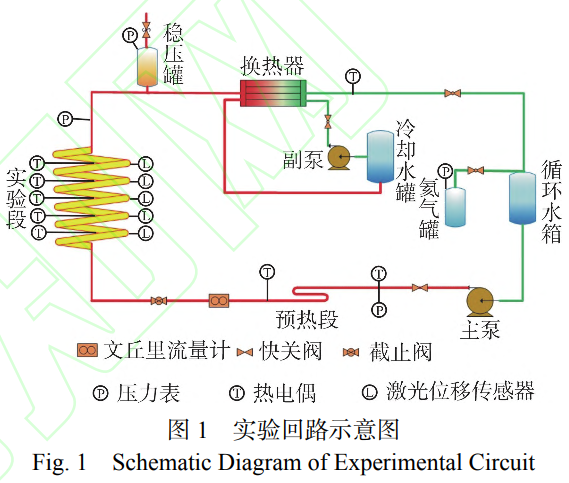
实验回路示意图,如图1所示。实验回路由一次侧实验回路与二次侧实验回路组成。一次测实验回路由主泵、预热段、实验段及管壳式换热器等主要部件组成。二次侧实验回路由冷却水箱、冷却水主泵及冷却塔组成,为一次侧实验回路提供热阱。实验工质为去离子水,实验中,去离子水由主泵流出经预热段进入实验段,然后流入管壳式换热器,最后流回主泵,形成闭式循环。实验中,主泵产生的热量会使得回路中去离子水温度上升,改变去离子水粘度从而影响实验结果,因此需要经由管壳式换热器带走额外热量,确保实验过程中去离子水温度稳定。此外,主泵运行时会产生振动,影响实验段振动响应特性。基于前期实验经验,实验段与实验回路间使用金属软管连接,以避免主泵远场激励的影响。
1.2实验本体
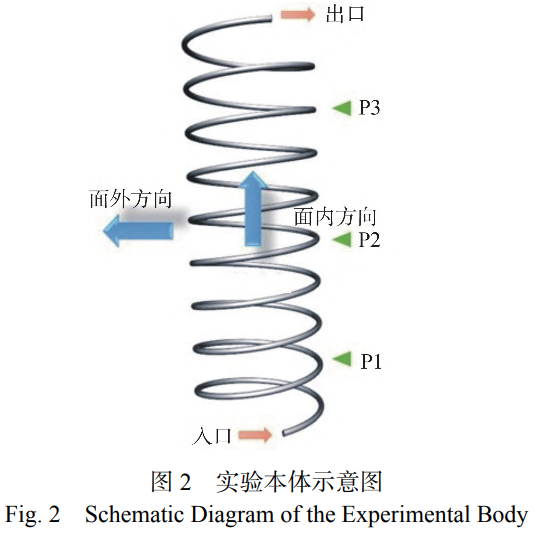
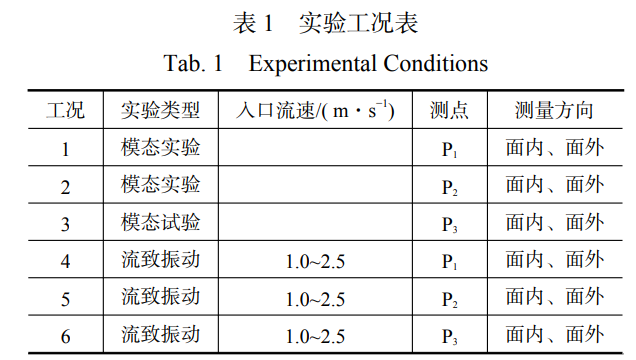
实验本体示意图,如图2所示。实验本体主要参数如表1所示。实验本体材质为316L不锈钢,螺旋直径与管道直径比为22.5,螺距为100mm,高度为900mm。实验本体两端布置约束装置,以线面接触的方式进行固定约束。
1.3测量方法
1.3.1测量仪器 实验本体入口布置有文丘里流量计,用于测量入口流量,误差为±0.067%。实验本体进出口装有T型铠装热电偶,用于测量实验本体进出口流体温度,精度为I级精度。实验本体振动响应特性由激光位移传感器测量得到,该仪器基于激光多普勒效应测量物体振动,位移分辨率为1.28nm,位移重复精度为1nm,最大速度量程为4500mm/s,采集频率最大可达2.5MHz。
1.3.2数据处理方法 振动位移实验结果用均方根(RMS)方法处理。本实验基于傅里叶变换将时域信号变换为频域信号。
1.4实验工况
本研究开展实验研究包括模态实验与流致振动实验,其中模态实验基于力锤敲击法开展,流致振动实验旨在探究不同入口流速对螺旋盘管振动响应的影响。测点P1高度为200mm、测点P2高度为500mm、测点P3高度为800mm。实验工况表见表1。
2、实验结果与分析
2.1模态分析
螺旋盘管的特殊结构导致其面内固有频率与面外固有频率存在差异,影响振动特性。通过开展模态实验,获得螺旋盘管面内与面外固有频率,结合静力学分析厘清质量效应对振动特性的影响规律,从而为管内单相流致振动响应分析提供参考。螺旋盘管各测点处面内方向固有频率均为8.7Hz,各测点处面外方向固有频率均为8.2Hz。本实验所用螺旋盘管刚度结构对称,因此各层盘管固有频率相同。由于螺旋盘管沿面内、面外方向刚度不同,因此沿面内、面外方向存在不同固有频率。为进一步明晰螺旋盘管振动特性,需要结合静力学分析探究质量效应对固有频率的影响。根据力学分析,可将单层盘管在面外方向上简化为等效具有等效质量自由振动弹簧系统,其固有频率表达式为:

式中,ωn为系统固有频率:k为系统刚度;m为系统质量。由表达式可知在面内向上固有频率仅与自身质量与刚度有关。在面内方向上,需将单层盘管简化为并联弹簧系统,同时还需考虑重力所致静变形的影响,受重力影响的并联弹簧系统静变形为:
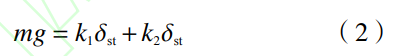
式中,δst为系统静态变形量;k1和k2为并联弹簧刚度;g为重力加速度。结合运动方程推导可得并联弹簧系统固有频率表达式:

由式(5)可知,在螺旋盘管面内方向上固有频率受静变形影响,这意味每层盘管面内方向的振动特性不仅受自身重力影响还会受相邻盘管推力与拉力影响。
2.2单相流致振动实验
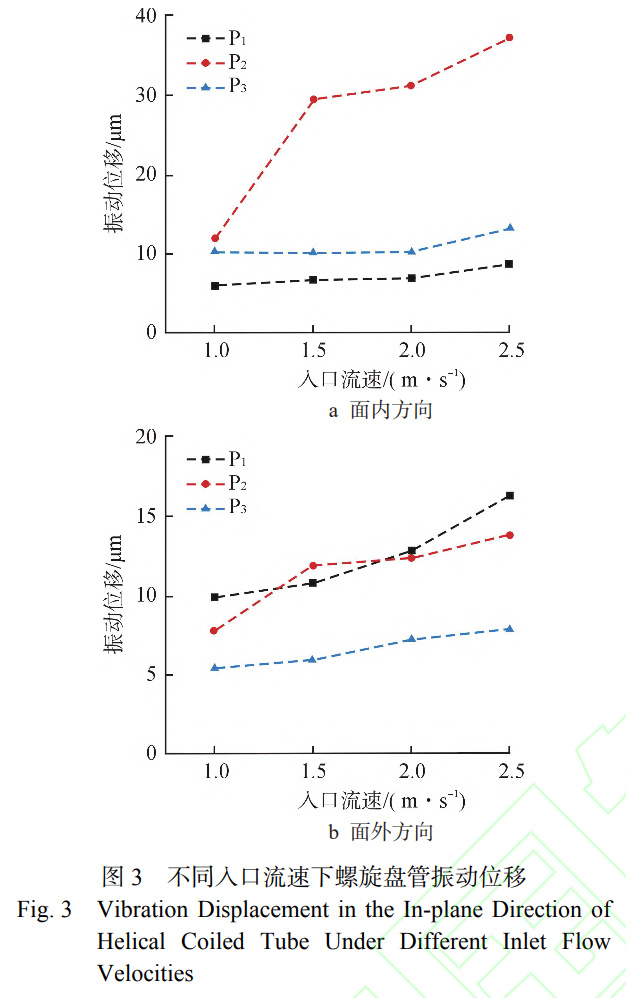
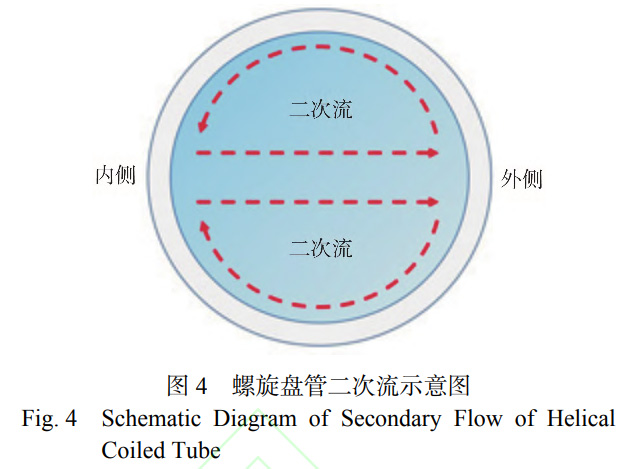
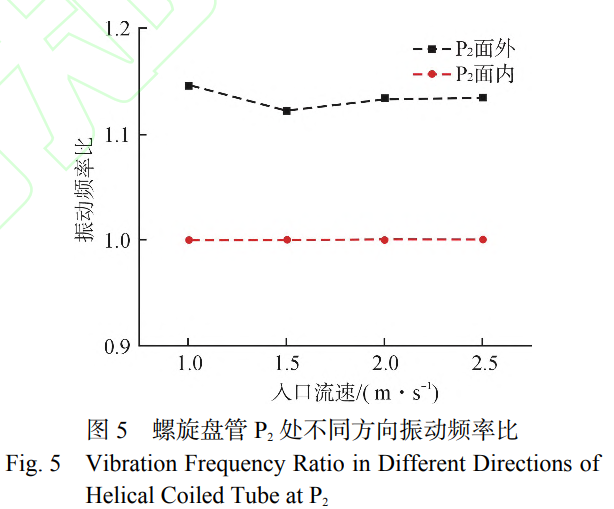
通过开展不同入口流速下管内单相流致振动实验,获得螺旋盘管各测点振动响应实验数据,结合模态分析结果,分析其振动规律与影响因素。螺旋盘管各测点面内方向振动位移如图3所示。由图3a可知,螺旋盘管面内方向振动位移随入口流速增加而增加,其中盘管中部(P2测点)测点处振动位移随入口流速的变化率约为16.9μm·(m·s−1)−1,远高于其他测点,其中P1处振动位移变化率约为1.8μm·(m·s−1)−1,P3处振动位移变化率约为1.9μm·(m·s−1)−1。由此可见螺旋盘管两端固支对振动位移具有明显的约束效果。由图3b可知,各测点面外方向振动位移演变规律与面内方向有明显差异。一方面,各测点振动位移变化率相近。另一方面,并未出现螺旋盘管中部振动位移明显高于两端的分布特征,P3处振动位移最小,P1与P2处振动位移相近,且在入口流速达到2.5m/s时P1处振动位移更大。导致上述现象的原因是螺旋盘管内特殊的流体流动状态,受离心力影响螺旋盘管内存在二次流动,当二次流动激励管壁时会产生振动响应。管内二次流示意图,如图4所示。二次流形成的根本原因在于流体在螺旋盘管内流动受到离心力影响,沿内侧至外侧方向移动导致。由此可知,当管内湍流度较强时,管内流体速度分布更加不均匀,从而产生更强的二次流动。在本次实验中,实验本体入口为螺旋盘管下端,当流体自下而上流过盘管时,受重力与流动摩擦影响,流体湍流强度逐渐下降,从而导致二次流动强度减弱,进而导致振动位移减小。因此,在螺旋盘管面外方向上振动位移随高度增加而减小,而P1与P2处振动位移相近是受支承约束影响导致。为进一步揭示面内与面外方向的振动响应机制,需要结合频域分析。通常,当结构振动频率与固有频率接近时,即认为振动响应发生锁定现象。螺旋盘管P2处,面内与面外方向振动频率比如图5所示。
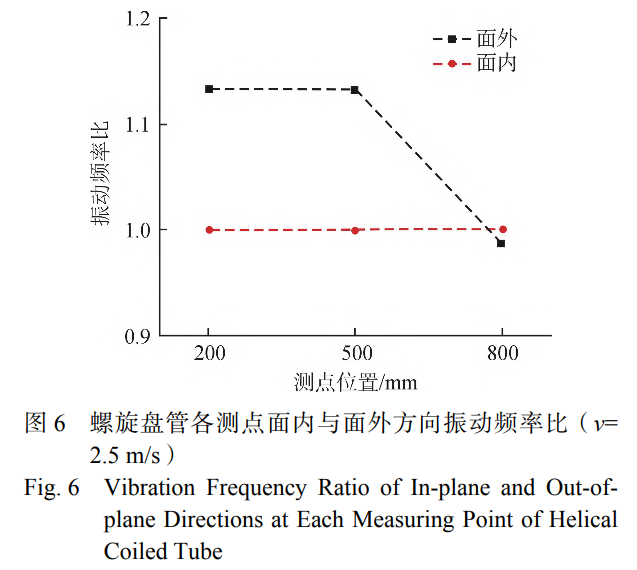
由图5可知,在面内方向上振动频率比均为1并不随入口流速变化,出现振动锁定现象。而面外方向上振动频率比均超过1,未发生振动锁定。2.5m/s入口流速下,螺旋盘管各测点面内与面外方向振动频率比如图6所示。由图6可知,在面内方向上不同测点的振动频率比均为1,出现振动锁定现象。而在面外方向上各测点均为出现振动锁定。结合图5与图6可知,螺旋盘管在面内方向上极易出现振动锁定现象,这意味着在面内方向上所受激励更接近于随机激励,其振动机制为管内流体的湍流脉动。
而在面外方向上振动频率与固有频率存在一定差异,因此推测面外方向振动响应与管内流体流动状态具有相关性。为验证上述分析,需结合频谱进行进一步分析。螺旋盘管P2处不同方向频谱如图7所示。
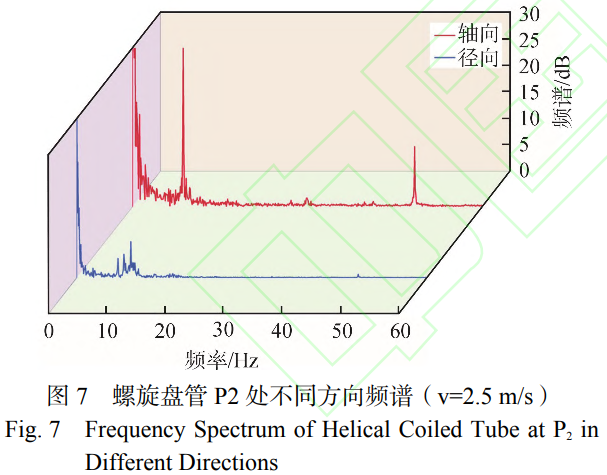
图7中红色曲线为面内方向振动频谱,其在固有频率(8.7Hz)附近的频率带宽较窄,仅存在8.7Hz的主要振动频率。由此可知,在面内方向上主要振动机制为管内流体的随机激励。根据面外方向频谱可知,即图中蓝色曲线,其在固有频率(8.2Hz)附近存在较宽的频带,6.7~11.5Hz,具有多个明显的振动频率,包括7.1Hz、8.1Hz和9.3Hz。由此可知,在面外方向上振动响应与管内流体流动状态相关,结合前文对二次流分析可知,管内二次流动为诱发面外方向振动的主要机制。为验证上述结论,需结合不同沿高度方向上不同测点频谱数据,假设管内二次流动强度或单位时间内的循环次数随高度的增加而减少,则螺旋盘管面外方向的振动频率也将随高速的增加而减少。螺旋盘管不同测点面外方向频谱如图8所示。
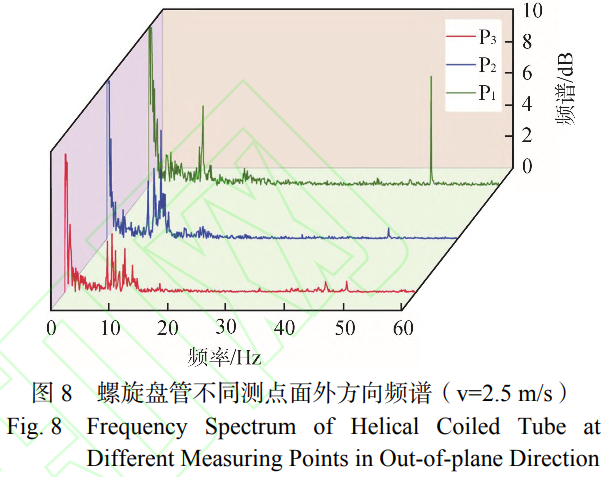
由图8可知,随着测点高度的增加,面外方向主振频率逐渐减小,由9.3Hz减小至8.1Hz,同时主振频率附近的频带呈现出展宽现象,并出现多个明显的振动频率。随着高度的增加,管内流体流速不均匀程度加剧,从而导致二次流流动状态不稳定,进而展宽振动频带形成多个明显振动频率。综上所述,在螺旋盘管面外方向上,管内二次流动是影响振动响应的主要机制。
3、结论
本研究基于激光多普勒测振技术,开展螺旋盘模态实验与管内单相流致振动实验,获得振动特性与振动响应,探究了螺旋盘管振动响应演变规律,揭示了两种振动机制,其主要结论如下:
(1)螺旋盘管在沿面外方向上振动特性受自身质量影响,在面内方向上同时受所受静力与质量影响。
(2)螺旋盘管面内方向振动位移受支承约束影响明显,而在面外方向上则主要受管内流体的二次流强度影响。
(3)螺旋盘管面内方向上的主要振动机制为管内流体随机激励,在面外方向上主要振动机制为管内二次流动。
参考文献:
[1]韩金盛,刘滨,李文强. 铅冷快堆研究概述 [J]. 核科 学与技术,2018, 6(3): 87-97.
[2] CIONCOLINI A, SANTINI L. Two-phase pressure drop prediction in helically coiled steam generators for nuclear power applications[J]. International Journal of Heat and Mass Transfer, 2016, 100: 825-834.
[3] HARDIK B K, PRABHU S V. Heat transfer distribution in helical coil flow boiling system[J]. International Journal of Heat and Mass Transfer, 2018, 117: 710-728.
[4]JO J C, JHUNG M J. Flow-induced vibration and frettingwear predictions of steam generator helical tubes[J]. Nuclear Engineering and Design, 2008, 238(4): 890-903.
[5]YUAN H M, SOLBERG J, MERZARI E, et al. Flowinduced vibration analysis of a helical coil steam generator experiment using large eddy simulation[J]. Nuclear Engineering and Design, 2017, 322: 547-562.
[6] PAÏDOUSSIS M P, LI G X. Pipes conveying fluid: a model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204.
[7] JUNG D, CHUNG J. In-plane and out-of-plane motions of an extensible semi-circular pipe conveying fluid[J]. Journal of Sound and Vibration, 2008, 311(1-2): 408- 420.
[8] JUNG D, CHUNG J, MAZZOLENI A. Dynamic stability of a semi-circular pipe conveying harmonically oscillating fluid[J]. Journal of Sound and Vibration, 2008, 315(1-2): 100-117.
[9]DELGADO M. An experimental study on flow-induced vibration of a single and adjacent tubes within a model helical coil heat exchanger[D]. College Station: Texas A&M University, 2021.
[10] PAÏDOUSSIS M P. Fluidelastic vibration of cylinder arrays in axial and cross flow: state of the art[J]. Journal of Sound and Vibration, 1981, 76(3): 329-360.
[11] TANG M, NI Q, WANG L, et al. Nonlinear modeling and size-dependent vibration analysis of curved microtubes conveying fluid based on modified couple stress theory[J]. International Journal of Engineering Science, 2014, 84: 1-10.
[12] IBRAHIM R A. Overview of mechanics of pipes conveying fluids —Part I: fundamental studies[J]. Journal of Pressure Vessel Technology, 2010, 132(3): 034001.
相关链接